Statistiques descriptives et regression linéaire

Dans ce chapitre, nous allon voir comment obtenir les principales statistiques descriptives de vos données. Nous allons ensuite aborder la mise en place d'une regression linéaire multiple, et comment tester la validité des hypothèse du modèle linéaire.

Analyse descriptive des données

La première étape pour analyser des données consiste en une analyse descriptive simple. Cela permet de mieux se familiariser avec les données que l'on manipule, et d'en repérer les principales caractéristiques : moyenne, variance, minimum, maximum, etc.

La fonction summary()

R dispose de la fonction summary() , qui permet d'obtenir toutes ses informations en un seul tableau. Prennons la base de données USArrests , fournie avec R et qui contient des informations sur le taux de criminalité des différents états américain. Cette base contient 50 observations (une par état) et 4 variables : le pourcentage de la population qui vit en zone urbaine, et les taux de crime, meurtre et agression (pour 100 000 habitants) de chat état.

Regardons les statistiques decriptives de ces données :

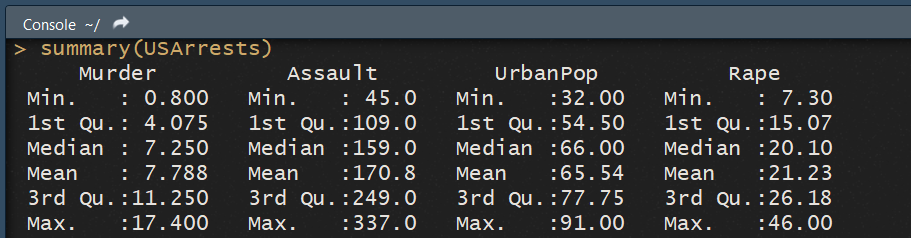
summary(USArrests)

La fonction summary nous donne 6 informations intéressantes :

• La valeur minimum prise par la variable.
• Le premier quantile.
• La médiane.
• La moyenne.
• Le troisiéme quantile.
• le maximum.

Cela permet d'avoir une première vue d'ensemble de nos données. On peut voir qu'il existe un large diversités pour toutes les variables. Le taux de population urbaine varie ainsi de 32% pour l'état le moins urbain, à 91% pour l'état le plus urbanisé. De même les différents taux de criminalités sont très variés. Ainsi si le taux de viol est en moyenne de 20 pour 100 000, 75% des états ont un taux inférieur à 26 pour 100 000, mais l'état le plus violent à un taux de 46 viols pour 100 000. A l'inverse l'état le plus sûr à un taux de seulement 7.3 viols pour 100 000.

La fonction summary() ne donne néanmoins pas certaines informations potentiellement importantes, comme la variance, ou la présence de données manquantes ou non.

La fonction describe() du package psycho

Pour compléter ce que nous apporte summary() , on peut utiliser la fonction describe() , fournie par le package psych. Si ce package est principalement conçu pour l'analyse des données en psychologie, sa fonction describe() est très intéressante.

Voyons ce qu'elle peut nous offrir comme informations complémentaires.

describe(USArrests)

On voit que l'on dispose déjà de plus d'informations, comme le nombre de données non manquantes, l'ecart-type, l'erreur-type, la skewness ou encore la kurtosis.

Avec ces deux fonctions summary() et describe() , nous pouvons avoir une première vue d'ensemble des caractéristiques de nos données.

La regression linéaire

Une des méthode d'analyse les plus classique est la regression linéaire. R propose pour cela la fonction lm() (pour linear model).

Essayons d'utliser une regression linéaire pour prédire le prix des logements à Boston. Le package MASScontient justement un data set nommé Boston avec les données qui nous intéressent.

install.packages("MASS")
library("MASS")

Regardons la structure de nos données :

str(Boston)

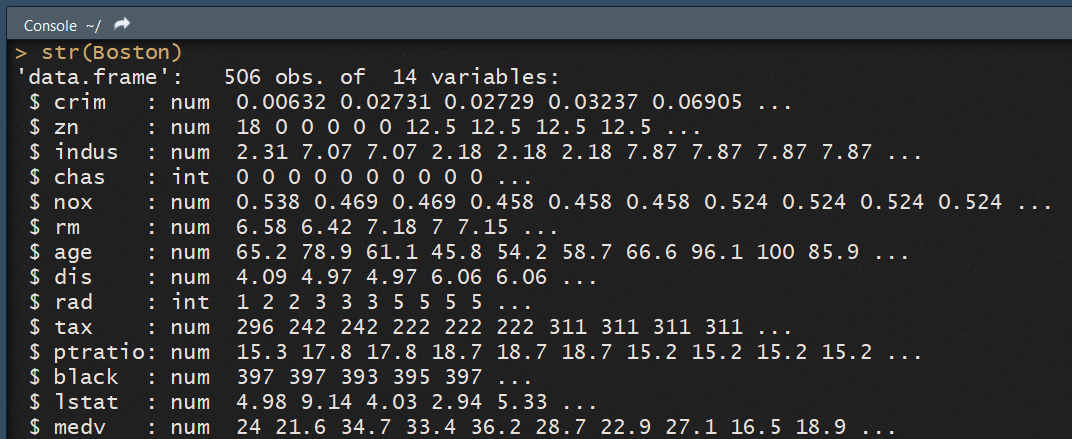Notre data frame est composé de 14 variables sur les différents quartiers de la ville de Boston. On retrouve entre autre parmis le prix médian des maisons d'un quartier (medv) le taux de criminalité pour 100 000 du quartier (crim), la concentration en polution nox , ou encore une variable indiquant la taxe d'habitation (tax ).

Une regression simple

La fonction lm() fonctionne de la façon suivante :

ma_regression = lm(variable_cible ~ predicteurs, data = mon_data_frame)

Pour commencer, voyons si en utilisant uniquement le taux de criminalité on arrive à une bonne prédiction des prix.

ma_regression = lm(medv ~ crim, data = Boston)

Si on exécute ce code, R nous créer une variable ma_regression qui est un modèle linéaire, contenant toute les informations sur notre regression. Pour obtenir les informations sur notre regression, on peut utiliser summary() appliquée à notre objet regression :

summary(ma_regression)

La console nous affiche alors toutes les informations sur notre regression : 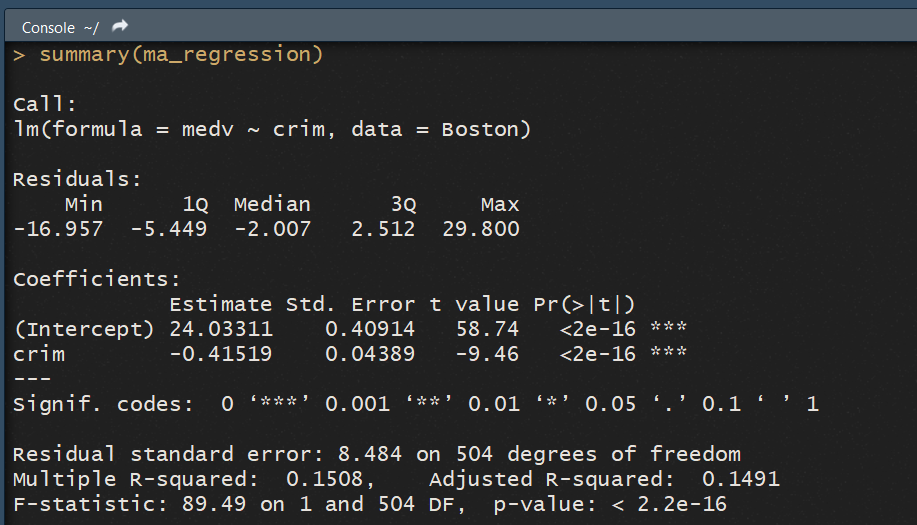La console commence par afficher avec Call la fonction que nous avons appelée pour la regression. Ici, la fonction lm() . Cela peut sembler redondant, mais si vous réalisez de nombreuses analyses avec différents modéles, cette information peut prendre du sens.

Ensuite la console nous donne des informations sur les résidus de la regression, via Residuals. Comme les résidus doivent être par hypothèse normalement distribués, on peut s'attendre à une médianne proche de 0 et à un max/min ainsi qu'un premier et troisième quartile proches en valeurs absolues. Ici, on constate que ces hypothèses ne sont pas vérifées, ce qui nous ammène à penser que notre modèle est un peu simpliste.

La consoloe affiche ensuite les coefficients du modèle, dans le paragraphe Coefficients . On y retrouve l'estimation de chaque coefficient, son ecart-type, la t-stats, ainsi que la p-value. Cette p-value est également accompagnée d'étoiles indiquant la significativitée du coefficient, comme la légende le précise.

Ici on peut voir en particulier que le signe du coefficient devant crim est bien négatif (avec une valeur de -0.41519), et que ce coefficient est bien significatif au seuil de 5% car la p-value est extrémement faible. Notre intuition que la criminalité à un impact sur le prix des logements est donc bien vérifiée.

Enfin, la console affiche les informations sur la standart erreur des résidus (residual standard error) et sur le R² de la regression. Nos résidus sont assez dispersés, avec une valeur de 8.44 (l'idéal étant 0, le modéle prédisant alors parfaitement). Le R² est disponible en version non ajustée (multiple R-Squared )et en version ajustée (Adjusted R-Squared ). Ici, les deux sont proches de 15%, ce qui veut dire que nous expliquons seulement 15% de la variation des prix, ce qui est relativement peu.

Enfin, la F-stat est affichée, afin de savoir si le modèle dispose au moins de coefficients non nulles. Ici, comme nous avons une seule variable, l'information est peu intéressante.

Regression multiple

La regression multiple fonctionne exactement comme la regression simple, si ce n'est qu'il suffit d'ajouter les variables en les séparants via un signe + . En plus du taux de criminalité crim , essayons de regarder si ajouter la polution nox et le niveau de taxes tax améliore la précision de notre modéle.

ma_regression = lm(medv ~ crim + nox + tax, data = Boston)

Regardons les paramétres de ce modèle :

summary(ma_regression)

On remarque nos résidus semblent toujours relativement proche de 0, avec une médiane à -2.5 et des valeurs allant de -4 à 2.5 entre le 1 et 3éme quartile. Cela pourrait-être mieux, mais à priori ce n'est pas problématique.

Intéressons plutôt aux coefficients du modèle. De façon intéressante, ils sont tous largement significatifs, et ont tous le signe attendu. La criminalité, la pollution et les taxes réduisent ainsi le prix des logements. Néanmoins l'effet des taxes semble être très faible, alors que à l'inverse la polution semble avoir un large impact.

Notre modèle est cette fois plus pertinent, avec un R² ajusté de 25% environ.

Mettre toutes les variables

Regardons ce que donne notre modèle si on incorpore les 13 variables explicatives disponibles. Pour cela il suffit d'écrire la regression en indiquant un . pour dire qu'on regresse sur toutes les autres variables :

ma_regression = lm(medv ~ . + nox + tax, data = Boston)

Regardons le résultat :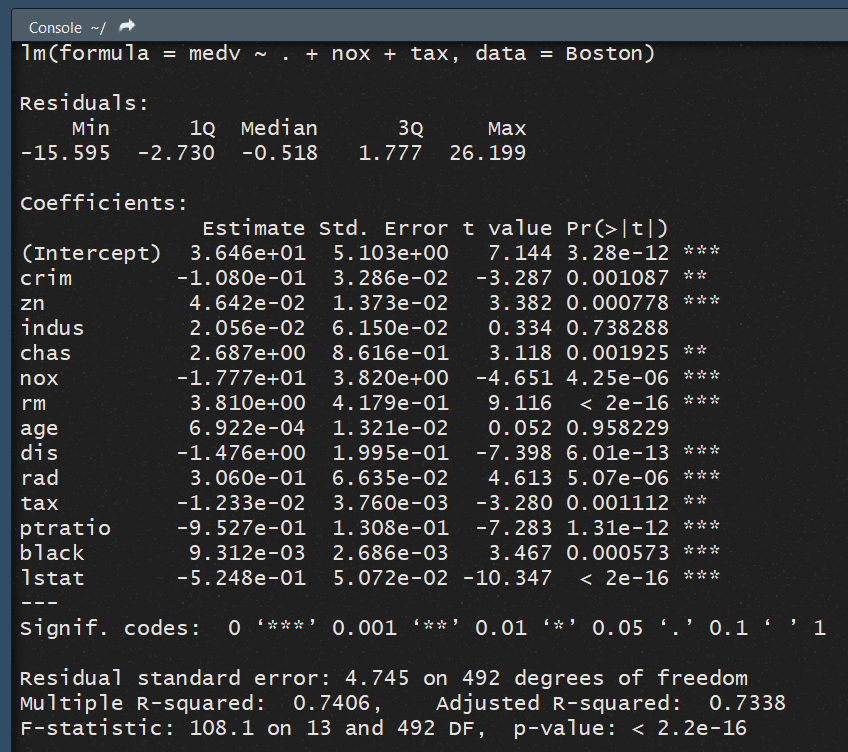On observe que les résidus sont bien plus proche de 0 cette fois. L'inclusion de certaines variables semble améliorer la qualité du modèle de ce point de vue.

Si on regarde les variable, on remarque que toutes sont significatives, sauf age et indus qui indiquent respectivement la proprotion d'immeubles anciens et d'industries dans la zone. Le R² de notre regression est largement satisfaisant : notre modèle explique 73% de la variation des prix dans la zone de Chicago.

Vérifier les hypothèses de la regression linéaire

Pour que notre modèle de régression linéaire soit valide, il nous faut vérifier que l'on respecte bien les hypothèses de base d'une regression. Un modèle linéaire suppose ainsi :

• Une relation linéaire entre les données (X) et la variable prédite (Y).
• Que les résidus sont normalement distribués.
• Que les résidus sont de même variance (homesédasticité).
• Que les résidus sont indépendants entre eux.

Nous devons vérifier si notre modèle ne rencontre par des problèmes comme de la non linéarité, de l'hétéroscedasticité, ou encore la présence de valeurs extrèmes, aussi bien dans les X que les Y.

Le package ggfortify fournit des fonctions pour permettre la visualisation des erreurs et permettre l'analyse graphique des regressions. Ces graphiques sont basés sur ggplot, comme le nom du package le laisse deviner. Nous allons également utilisé le package lmtest qui fournit un certain nombres de fonctions utiles pour tester les modèles linéaires. Ainsi nous aurons à la fois une approche visuelle intuitive, et une approche statistique de la validité (ou non) de nos hypothéses.

Installons et chargons ces deux packages :

install.packages(c("ggfortify", "lmtest"))
library(c("ggfortify", "lmtest"))

Utilisons maintenant la fonction autoplot() de ggfortify pour avoir les principaux graphiques qui vont nous aider à diagnostiquer notre modèle.

ma_regression = lm(medv ~ ., data = Boston)
autoplot(ma_regression)

La fonction affiche quatre graphiques, que l'on désignera par les numéros indiqués :

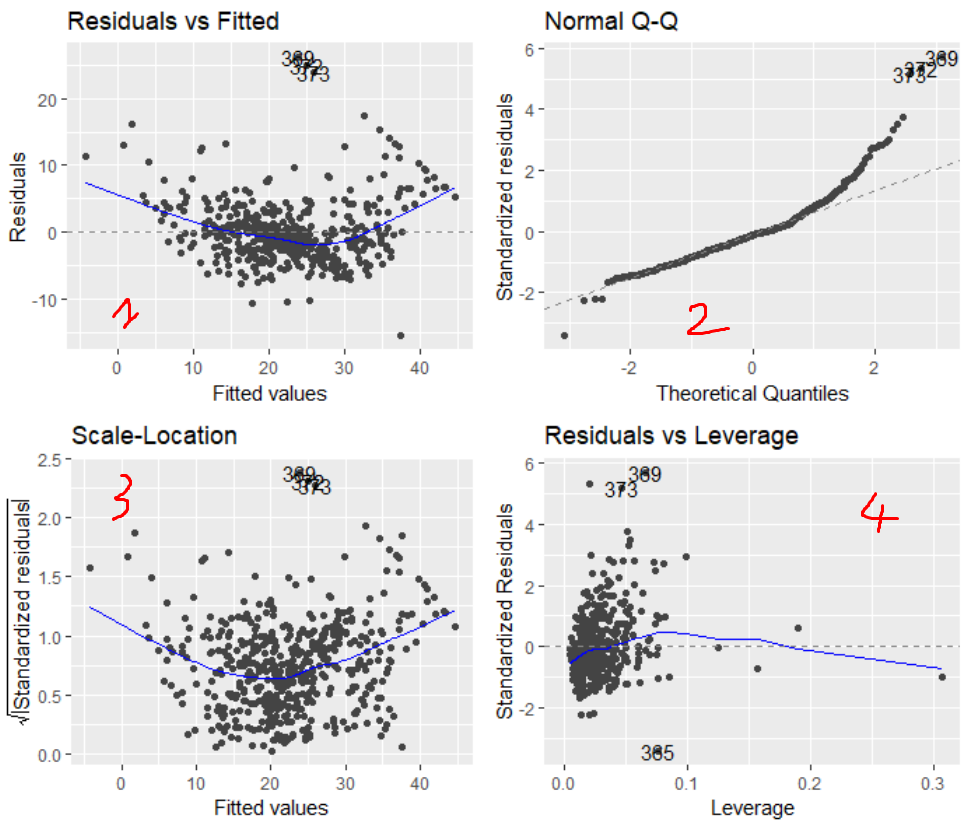
Expliquons le principe de chacun.

• Residuals vs Fitted : affiche les résidus en ordonnée et la valeur prédite par le modèle en abscise. Normalement l'erreur doit être indépendante des valeurs précites Y, donc les points doivent se distribuer autour de 0 de façon aléatoire. La ligne bleu de regression doit être horizontale en théorie.
• Normal Q-Q : Ce graphe nous renseigne sur la distribution normale des résidus. Affiche la distribution des résidus (normalisés) par quantiles. La ligne en pointiés indique la répartition que les résidus doivent suivre si ils sont normaux. En théorie, ils doivent donc suivre la ligne.
• Scale-Location : Ce graphique est du même type que le premier graphe, si ce n'est qu'il représente l'eccart-type des résidus en fonction de la valeur prédite. Cela nous permet de vérifier l'hypothèse d'homoscedasticité, qui doit conduire à une ligne bleue horizontale.
• Residuals vs leverage : Ce graphe nous permet de visualiser les valeurs outliers qui impactent la regression. nous le décrirons plus en détail en dessous.

De plus, pour chaque graphique, R nous affiche les numéros des observations les plus extrèmes, pour nous permettre d'aller voir manuellement de quoi il en retourne.

Interprétation des graphiques et tests statistiques :

Chaque graphique va nous permettre de vérifier une des différentes hypothèse de notre modèle de regression linéaire. Nous ferons également certains tests statistiques de base quand cela sera intéressant pour confirmer notre analyse graphique.

Linéarité des données

Le premier graphique nous renseigne sur la linéarité des données.

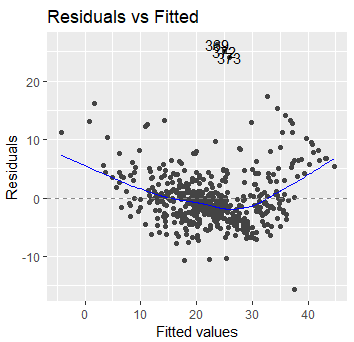
Si les valeurs préditent sont bien linéaires des données, alors l'erreur ne doit pas être corrélée à la valeur prédite. La ligne bleue de regression devrait donc être horizontale. Ici on voit que notre modèle à un problème avec les faibles prix et les prix élevés. Il semblerait que la relation soit plus polynomiale que linéaire.

Remarque : En réalité, les modèles polynomiaux sont plus efficaces pour prédire les prix des logements que les modèles linéaire. Nous en avons la confirmation visuelle ici. Bien que notre modèle ai un R² de 75%, il est évident que une spécification polynomiale permettrait encore de l'améliorer.

En fonction de la forme prise par la courbe bleu, différentes transformation des données peuvent sembler plus ou moins intuitives à utiliser.

Homosédasticité de la variance

Le troisième graphique nous renseigne sur l'homogénéité de la variance des résidus.

Normalement, la variance des résidus est indépendante de la valeur prédite par le modèle. Si le modèle est correct, la ligne bleue doit être horizontale. Clairement, nos résidus ne sont pas du tout homogènes. On retrouve là encore un patern polynomiale : la variance des résidus est beaucoup plus élevée pour les faibles et hautes valeurs.

On retrouve aussi trois points (les observations 389, 372, et 373) qui semblent être des outliers, avec des variances trés fortes. Là aussi, une solution consiste à transformer les données. Une transformation de Box-Cox est souvent pertinente et permet de trouver automatiquement la fonction de transformation adaptée pour rendre les résidus normaux.

On peut tester l'hypothèse d'homosédasticité avec un test de Breusch-Pagan, qui est implémenté dans le package lmtest via la fonction bptest(). Il nous suffit de lui donner le modèle en paramètre :

bptest(ma_regression)

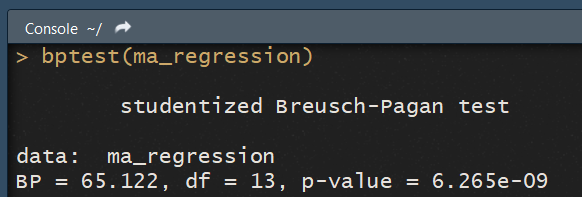
On peut rejeter l'hypothèse d'homosédasticité des résidus, qui est l'hypothèse nulle, si la p-value est inférieur à notre seuil de significativité. Ici, avec une p-value de 6.25e-09 , l'd'homosédasticité est largement rejettée. Notre intuition graphique est bien confirmée par l'analyse statistique.

Normalité des résidus

Le second graphique nous permet d'étudier visuellement la normalité des résidus.

Si les résidus sont distribués normalement, ils doivent se distribuer selon la ligne en pointiés. Là encore, on retrouve le même problème que précédement avec les valeurs extrêmes, en particuliers du coté positif. Le coté négatif est moins éloigné. A partir de 2 ecarts-types, il y a beaucoup trop de valeurs extrêmes du coté positif de la distribution, avec certaines valeurs etrêmes.

On peut tester la normalité des résidus de façon plus formelle avec un test de Shapiro-Wilk. R dispose d'une fonction intégrée pour cela, qu'il suffit d'appeler en lui passant le vecteur d'erreurs en paramétre :

shapiro.test(errors)

On constate alors via la p-value que l'hypothèse nulle de normalité est largement rejetée . Notre intuition graphique de non normalité des résidus est largement rejettée :

Identifier les valeurs extrêmes et les high leverage points

Les valeurs extrêmes (outliers) sont des valeurs bien plus grandes que les autres de la variable prédite. Si la prédiction est trop loin des vrais valeurs, alors cela pénalise le modèle et augmente fortement le RSE. De plus, cela impact artificiellement la pente de la regression, qui essaye de prendre en compte ces valeurs. Il est donc important de prendre en compte ces valeurs.

Pour les identifier, on va utiliser les résidus standardisés. En regardant à combien d'ecart-type un résidus se situe, on peut voir si on est en présence de valeur etrême ou non. En général on considére que plus de 3 (parfois 4) ecart-types caractérisent la présence d'une valeur extrême.

Les high leverage points représentent eux les points pour lesquels les variables prédictives sont extrêmes. Par exemple un quartier de Boston avec une taxe d'habitation bien plus élevée ou faible que les autres pour des raisons historiques, qui impacterait alors notre regression. Pour observer ses valeurs, on peut le levier statistique (statistic leverage). On considére que le levier d'une observation est important si il est supérieur à 2(p + 1)/n avec p le nombre de variables et n le nombre d'observations. Ici ce seuil est de 2(13 + 1)/506 soit 0,055 .

On voit ici que un certain nombre de données sont à plus de 3 ecart-types, et que une partie non nulle d'observation dispose d'un leverage supérieur au seuil défini. Il est probable dans notre cas qu'il s'agisse des variables extrêmes, qui posaient problémes au niveau de la normalité des résidus. On observe en effet que les variables problématiques se concentrent plutôt en haut à droite du nuage de point, confirmant cette intuition.

Valeurs influente

On peut résumer la façon dont une observation influence la regression via une combinaison de son levier et de la taille de son résidu. La distance de Cook nous permet de mesurer cette influence. Cela permet de trouver les points qui sont a priori abérants et qui ont une réelle influence sur le modèle. En effet, un point peut-être abérant mais ne pas réellement avoir d'influence sur la qualité du modèle.

Utilisons la fonction de base de R plot pour cela :

plot(model, 4)

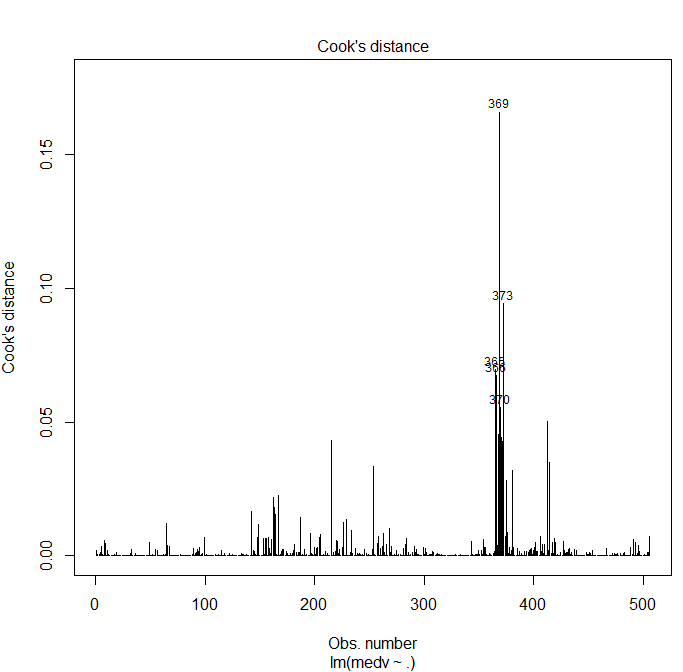
Le graphique obtenu est certe moins beau qu'avec ggplot, mais il nous conviendra. La distance de cook est trop grande si elle dépasse 1, ce qui n'est pas le cas ici. Nous retrouvons néanmoins le même groupe de 4 variables problématiques déjà identifiées sur les graphiques précédents, ce qui laisse penser que ces variables sont potentiellement en partie des outliers.

Test d'auto-corrélation des résidus

Enfin, nous allons tester l'auto-corrélation des résidus. Pour cela, nous utiliserons le test de Durbin-Watson, via la fonction dwtest() du package lmtest .

dwtest(ma_regression)

Ce test pose pour hypothèse nulle que les résidus ne sont pas corrélés. Par conséquent, si la p-value est inférieur à un seuil alpha = 5%, on peut jetter cette hypothése.

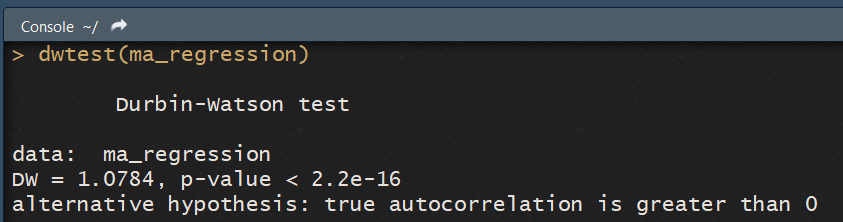La console nous indique même l'hypothèse alternative à "accepter", ici que l'autocorrélation est supérieure à zéro (le package choisit lui-même l'hypothèse alternative qui explique le mieux les données).

Conclusion de notre analyse :

Nous avons vu les principales façon de tester les hypothèses du modèle de regression linéaire. Rapidement nous avons remarqué que ces hypothèses n'étaient pas respectées, probablement en raison d'un patern non linéaire dans les données. Bien que notre regression garde un bon pouvoir explicatif (via un r² élevé), utiliser un modèle polynomial serait probablement plus pertinent encore.

La regression logistique