2.1 Représenter et manipuler les nombres en R

Pour commencer en douceur, regardons comment nous pouvons utiliser R pour représenter et manipuler des nombres. R permet de travailler facilement avec les nombres, qu'ils soient entiers, négatifs, décimaux ou même complexes. Pour un langage dédié à l'analyse statistique, c'est plutôt rassurant non ? Les nombres sont ainsi le premier type d'objets que nous allons rencontrer.

Les différents types de nombres

R possède en réalité trois types d'objets différents pour représenter les nombres, selon la nature du nombre en question.

• Le type integer représente les nombres entiers (integer signifiant entier en anglais).
• Le type double représente les nombres réels.
• Le type complex représente les nombres complexe comme son nom l'indique.

Trois types pour représenter les nombres ? Cela peut sembler compliqué au début, mais vous allez rapidement vous y faire. Voyons comment écrire différents nombres dans la console et les manipuler.

Les nombres entiers, ou le type "integer" :

Commençons avec les nombres entiers. Pour écrire un nombre entier en R, il suffit d'écrire un nombre, puis d'écrire la lettre L collée juste après, comme ceci :

10L #le nombre entier 10

Si vous écrivez un tel nombre dans la console, R va simplement vous l'afficher en retour, comme ceci :

On peut déjà remarquer que la console n'affiche pas le L après notre nombre, alors que nous entrons pourtant 10L . En effet, ce L est uniquement là pour faire comprendre à R que l'on souhaite écrire un nombre entier. R sait bien que 10L représente le nombre 10 , et nous l'affiche donc en tant que tel. Nous verrons un peu plus tard l'intêret de ce L.

Vous pouvez essayer d'entrer d'autres nombres de type integerdans la console, elle vous affichera toujours le nombre en question. Afficher des nombres dans la console c'est pas très intéressant en soi, mais une fois que nous aurrons vu les différents types de nombres, nous pourrons commencer à réaliser des opérations entre eux. Et dans le chapitre suivant, nous apprenderons à stocker les résultats de nos calculs. En attendant, continuer à apprendre les différentes façon de représenter des nombres en R.

Les nombres réels, ou le type "double" :

Pour représenter les nombres réels, R utilise le type double. Un nombre de type double s'écrit en R de façon "normale", simplement en utilisant un . pour écrire les décimales :

3.14 #Le nombre décimal 3.14

Plutôt facile non ? Comme pour les entiers, la console nous affiche simplement le nombre que l'on vient d'écrire :

Le type double permet aussi de représenter les nombres entiers. Vous pouvez simplement écrire un entier comme un nombre dont la partie décimale est nulle, comme ceci :

3.0 #le nombre entier 3 de type double

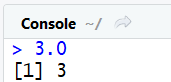
Comme vous pouvez le voir, la console affiche directement le nombre 3 , sans montrer les zéros inutiles.

Vous pouvez aussi ne pas écrire la partie décimale. R va alors comprendre de lui même que la partie décimale est nulle et vous voulez représenter un nombre entier de type double :

3 #l'entier 3 de type double

Cette forme d'écriture à l'avantage d'être bien plus pratique que d'écrire une partie décimale nulle.

Ainsi, si on écrit des nombres entiers sans ajouter de L , R les comprendra comme des nombres de type double avec une partie déciminale nulle, et non comme des entiers de type integer . C'est la raison pour laquelle les integer s'écrivent avec le L : pour les différencer des entiers de type double !

Remarque : Dans la console, les nombres entiers de type integer s'affichent exactement de la même façon que les nombresdouble . Ainsi 3L s'affiche exactement de la même façon que le double 3 . Pour éviter les confusions nous indiqueront toujours le L aprés un integer , même si en réalité il ne sera pas affiché.

10L #affiche 10L
 #La console affiche "10", mais cette écriture permet de voir qu'on parle d'un integer

Pourquoi ce nom de double ?

Finissons de présenter les nombres de type double avec un autre petit détour historique pour en expliquer le nom.

Pourquoi appeler double le type de données représentées par les nombres décimaux ? Ce nom remonte simplement aux orgines de l'informatique, où les ordinateurs avaient une mémoire très faible. Il fallait alors stocker l'information en utilisant le minimum de place possible. Avec l'évolution de la technique, on à pu stocker des nombres plus grand, et certains langages ont décidé d'appeler double les nombres réels stockés sur 64 octets de mémoire, alors qu'avant il était courant de les stocker sur seulement 32 octets. Ces nombres réels étaient ainsi deux fois plus précis que les anciens, car on pouvait retenir le double de décimal ! D'où le terme de "double", pour nombre réelle avec une précision doublée. Depuis, ce nom de double est resté dans de nombreux langages pour désigner les nombres réels, quand même bien ils ne seraient pas stockés sur 64 ocets ou qu'il n'existai pas de type "simple" prenant deux fois moins de mémoire d'un double !

R étant là aussi un langage relativement ancien ayant hérité de S, il à conservé cette appelation désuete de double pour désigner les nombres réels.

Les nombres complexes, ou le type "complex" :

Le troisiéme et dernier type de nombres que nous pouvons rencontrer est les nombres complexes. Il s'écrivent de façon trés intuitive, en se composant d'une partie entiére et d'une partie imaginaire comme attendu :

5 + 2i #Un nombre complexe

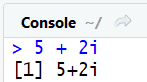
Attention à petit point de détail : si vous voulez représenter le nombre i seul, vous devez ajouter un 1 devant, pour bien préciser que vous parlez de une fois le nombre imaginaire :

#Il ajouter ajouter un 1 devant le i : 
5 + 1i #Un nombre complexe 
1i #seulement une partie imaginaire

Pourquoi trois types de nombres ?

Il est facile de comprendre à quoi servent les nombres de type complex . Mais pourquoi avoir deux autres types de nombres (integer et double ), alors qu'on peut trés bien représenter les nombres entiers avec le type double ?

La raison est historique. Ecrire un entier sous la forme d'un integer prend (un peu) moins de place en mémoire que le même entier sous forme de double. A une époque où les ordinateurs avaient peu de place en mémoire, il pouvait être important de faire la différence entre les types de nombres pour optimiser un programme. Un programme qui utilisait beaucoup de nombres entiers et les comptait comme des doubles au lieu de integer gaspillait de précieuses ressources en mémoire.

De nos jours, cette différence d'utilisation de mémoire est totalement negligeable pour nos ordinateurs modernes. Il faudrait manipuler des millions de nombres en même temps pour que votre ordinateur personnel puisse voir la différence ! Mais comme R est un langage assez vieux, il à hérité de cette distinction qui était courante dans les premiers langages informations.

En pratique, nous n'utiliserons pas le type integer , qui demande l'effort d'ajouter un L à chaque nombre, et qui n'a plus vraiment d'utilité de nos jours. Nous écrirons uniquement des double , plus rapide à écrire, et sans que cela n'ai d'impact visible sur nos ordinateurs modernes.

Connaitre le type d'un objet avec la fonction typeof() :

Nous venons de voir les trois types d'objets qui permettent de représenter des nombres en R : integer , double et complex . Il est parfois utile de pouvoir vérifier le type du nombre ou de la donnée que l'on manipule, pour s'assurer que l'on travaille bien avec le type que l'on souhaite. Il existe pour cela la fonction typeof() , qui renvois le type la donnée placée entre parenthèses. Voici un exemple d'utilisation pour vérifier le type d'un nombre integer :

typeof(10L) #affichera "integer" dans la console

La fonction nous affichera alors dans la console le type de la donnée en question, ici un nombre entier de type integer .

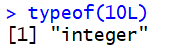
Nous sommes donc bien sur que l'objet que nous manipulons est un objet basique de type integer .

Vérifions aussi que les autres types de nombres produisent bien le résultat attendu et que typeof() affiche leur type : double et complex :

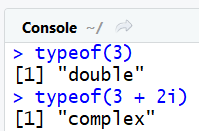
Remarquez que le nombre 3 est bien un double , bien qu'il soit un entier ! Les entiers au sens courant du terme peuvent être représentés en R soit par des integer (comme 1L , 3L ), soit par des double (comme 1 ou 3.0 ).

Cette fonction typeof() nous servira tout au long de ce cours pour connaitre la nature des objets représentrée dans nos programmes. En effet, elle fonctionne pour les types de nombres, mais aussi pour tous les autres types de données/objets que nous allons décourir au fur et à mesure de notre progression. Aussi, essayez de vous en souvenir !

Manipuler des nombres et calculer des expressions mathématiques

Maintenant que nous avons vu les trois types de nombres en R, nous allons voir comment les utiliser pour réaliser des calculs mathématiques. R permet de manipuler les nombres facilement avec les opérations de base. Une chose importante à retenir est que pour qu'une opération fonctionne, il faut toujours que les éléments soient de même type : on ajoute les integer avec les integer , les double avec les double et les complex avec les complex . R est un langage qui aime bien l'ordre.

Les opérations usuelles :

Voici les opérations mathématiques uselles que l'on peut réaliser en R. Comme vous pouvez le voir, leur écriture est intuitive. La console affiche directement le résultat de notre opération.

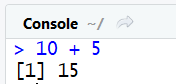
Addition :

10 + 5 #addition (affiche 15)

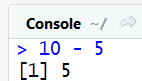
Soustraction :

10 - 5 #soustraction (affiche 5)

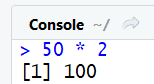
Multiplication :

50 * 2 #multiplication (affiche 100)

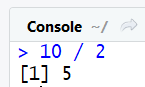
Division :

10 / 2 #division (affiche 5)

Puissance :

10^3 #puissance (affiche 1000)

Modulo et division arrondie

R sait également faire deux autres opérations intéressantes, qui peuvent être utiles dans certaintes situations. Il s'agit du modulo , qui est le reste aprés la division entiére, et de la division avec arrondie à l'entier inférieur.

Modulo :

10 %% 3 #modulo (affiche 1 car il reste 1 aprés la division entiére de 10 par 3)

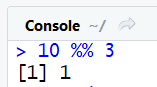
Attention, l'opérateur pour calculer un modulo est bien composé de deux signes % , si vous en utilisez un seul R ne comprendra pas le sens de votre calcul et vous indiquera une erreur.

Division arrondie :

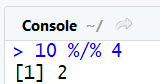
10 %/% 4 #division avec arrondi à l'entier inférieur (affiche 2)

La gestion des priorités et des parenthèses

R reconnait automatiquement l'usage des parenthèses dans les calculs et applique la priorité conventionnelle lors des opérations. Vous pouvez ainsi écrire des calculs sophistiqués, R utilisera les bonnes régles de priorité pour donner le résultat attendu.

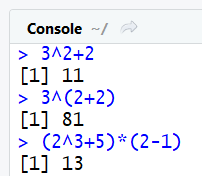
3^2+2 #donne 11, la priorité de la puissance est bien respectée
3^(2+2)#donne 81, la priorité des parenthèses est bien respectée
(2^3+5)*(2-1) #Donne 13 la priorité des parenthèses est bien respectée

La gestion des infinis et des formes indéterminées :

R est non seulement capable de réaliser les calculs correctement, mais il sait aussi comment gérer les cas problématiques, comme ceux qui produisent un résultat infini (comme la division par 0), ou ceux qui produisent un résultat indéterminé (comme divisé l'infini par l'infini). Regardons ceci de plus prêt !

Les formes infinies :

R est non seulement capable de réaliser les calculs correctement, mais il sait aussi travailler avec l'infini. Il utilise les "nombres" Infet -Infpour représenter l'infini et moins l'infini.

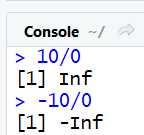
#Diviser par 0 donne Inf
10/0 
#Diviser un nombre négatif par 0 donne -Inf
-10/0

R est également cohérent quand on essaye de manipuler l'infini. Ainsi ajouter $$+ \infty + \infty$$ donnera bien $$+ \infty$$, idem pour moins l'infini.

#On enlève 1000 à l'infini
Inf - 1000
#on ajoute l'infini
Inf + Inf 
#On ajoute moins l'infini 
-Inf -Inf

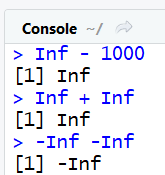
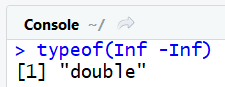
Remarquez que Inf est bien considèré comme un nombre par R, et plus précisément un nombre de type double :

typeof(Inf) #double

Ceci est aussi vrai pour -Inf .

Résultat indéterminé et NaN :

Que ce passe-il si on essaye une forme indéterminée, comme par exemple ajouter plus l'infini moins l'infini ? Alors R retournera NaN pour Not a Number (pas un nombre), indiquant que l'opération demandée de donne pas de résultat déterminable.

#plus l'infini moins l'infini donne une forme indéterminée :
Inf -Inf #donne NaN
# L'infi multpliée par 0
Inf*0 #donne NaN

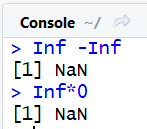
NaN est bien un objet de type nombre, plus précisement de type double, exactement comme ses compères Infet -Inf :

typeof(Inf -Inf) #double

Propagation des NaN :

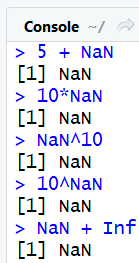
Toute opération qui implique NaNdonnera également comme résultat NaN. En effet ajouter un nombre avec quelque chose d'indéterminé donnera aussi une indétermination. On dit alors que NaNse "propage" dans le calcul car tous les calculs où il sera impliqué donneront également NaN. Tous ces exemples auront ainsi pour valeur NaN :

#Addition :
5 + NaN
#Multiplication :
10*NaN
#Puissance :
NaN^10
10^NaN 
#Nan est plus fort que l'infini :
NaN + Inf

L'infini, NaN et les complexes :

Remarquez que les nombres complexes peuvent avoir dans des cas d'intermination une partie réelle ou imaginaire infine, et l'autre partie NaN. Regardons un exemple :

1 + Inf*1i)*5 #On peut multiplier i par l'infini comme les deux sont des nombres
#Cela donne le nombre complexe NaN+Infi

On voit que le résultat est bien Nan + Inf*i ce qui correspond au calcul correct et est bien un nombre complexe car composé d'une partie réelle et imaginaire (n'oubliez pas que NaNet Infsont des doubles).

Vous pouvez ainsi utiliser R comme une véritable calculatrice de façon trés intuitive, qui gère à la fois différents types de nombres, les régles usuelles de prioriété et de calcul, ainsi que les formesinfinies et indeterminées.

R et la précision des calculs

Comme tous langage informatique, R ne peut représenter de façon exacte des nombres qui ont un nombre infini de décimale, comme le nombre pi ou racine de 2. En effet, un ordinateur ayant une mémoire finie, il ne peut stocker un nombre infini de nombres après la virgule. Cela est matériellement impossible.

Ces nombres seront donc toujours arrondis avec une plus ou moins grande précision et les résultats obtenus lors de tels manipulations ne pourront par nature jamais être exacts.

Mais ce problème est plus subtile qu'il n'y parrait. R représente les nombres non pas en base décimale comme nous, mais en base 2, c'est à dire comme une suite de 0 et de 1. Ainsi le nombre 100 s'écrit 1100100 en binaire. Hors, certains nombres qui ont une écriture décimale finie comme 0.1 en base décimale, ont une écriture binaire infinie (comme 1/3 peut l'avoir en base décimale). Aussi ce n'est pas par ce que vous manipuler des nombres qui ont l'air d'avoir une écriture finie en écriture décimale, que c'est forcement le cas du point de vue de R !

Sans entrer dans les détails, l'affiche de la console de R se débrouille pour cacher les petites erreurs de calcul que cela peut entrainer. Ainsi la plupart du temps nous pensons obtenir un résultat exact, alors que ce n'est pas le cas ! Par exemple 1/10 s'affichera correctement dans la console de R, mais la représentation interne stockée en mémoire sera elle inexacte, car ce nombre n'a pas d'écriture finie en binaire.

De façon générale, il faut toujours être prudent quand on manipule des nombres réels en informatique : dans de nombreux cas, les résultats ne pourront pas être exacts et entraineront des erreurs d'arrondi, qui seront plus ou moins grave. Il existe des méthodes spécifiques pour réaliser du calcul scientifique avec une grande précision, mais cela n'entre pas dans le cadre de ce cours. Il est important que vous gardiez à l'esprit que les calculs avec des réels sont rarement totalement exact en R, et que parfois cela peut entrainer des résultats inatentus dans nos programmes. Nous y reviendrons sur le chapitre sur les expressions.

A retenir :

• Il existe trois types de nombres en R : integer pour les entiers, double pour les réels et complexe pour les nombres complexes.

• On peut connaitre le type d'un élément de cette façon : typeof(element). Le type s'afficher alors dans la console.

• Toutes les opérations mathématiques usuelles fonctionnement correctement en R, et doivent se faire entre élèments du même type.

• R gère correctement les régles de priorité du calcul mathématique, en particulier les formes infinies qui donnent Infou -Infet les formes indéterminées qui donnent NaN pour Not a Number. Tous sont de type double et sont donc considérés par R comme des sortes de nombres !

• Comme tous langage informatique, R ne peut gérer correctement les nombres avec une écriture binaire infinie, comme pi ou 0.1. En pratique cela conduit à des approximations, qui peuvent parfois conduire nos programmes à donner des résultats inatendus.