3.5 Manipuler les matrices

Nous avons vu comment créer des matrices au chapitre précédent, et découvert la différence entre la class et le type d'un objet. Nous allons maintenant approfondir nos connaissances sur les matrices et voir comment les manipuler.

Nommer les lignes et les colonnes d'une matrice

Supposons que nous voulons entrer dans une matrice les notes d'examens de plusieurs étudiants : Pierre, Paul, Marie et Anna. Commencons par créer une matrice à partir des vecteurs des notes sur 20 des étudiants.

pierre = c(12, 9, 18, 15)
paul = c(15, 8, 12, 14)
marie = c(13, 17, 15, 14)
anna = c(12, 15, 17, 18)
notes = matrix(data = c(pierre, paul, marie, anna), nrow = 4, byrow = TRUE)

Notre matrice de notes n'est pas trés lisibles comme ceci :

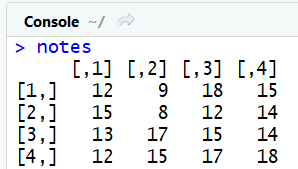
Pour arranger cela, on peut nommer les lignes et les colones de la matrice à l'aide des fonctions rownames() et colnames() . Nommons en ligne le prénom des étudiants, et en colonne les matiéres.

rownames(notes) = c("Pierre", "Paul", "Marie", "Anna")
colnames(notes) = c("Français", "Histoire", "Economie", "Mathématiques")
print(notes)

Et voici le résultat ! Plus facile à lire non ?

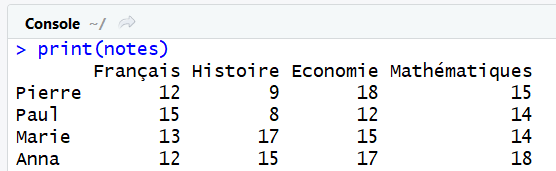
Selectionner des éléments dans une matrice

Nous allons voir comment selectionner un ou plusieurs éléments dans une matrice, que ses lignes et colonnes soient nommées ou non.

Selectionner un élément

Pour selectionner un élément dans notre matrice, il nous faut ses coordonées. Comme en mathématique les coordonnées commencent par le numéro de ligne i et le numéro de colonne j . On peut alors selectionner un élément avec la syntaxe ma_matrice[i,j] .

Selectionner la note d'économie de Marie :

notes[3, 3] #affiche 15

Cette façon de faire est efficace, mais peu lisible : il est impossible à la lecture du code de savoir quel étudiant et quelle matiére sont selectionnées. Heureusement il existe une autre syntaxe dans le cas des matrices dont les lignes et les colonnes sont nommées.

Selectionner un élément nommé

Si notre matrice est nommée (comme dans notre exemple), il est possible d'utiliser le nom des colones et des lignes pour accéder à un élément. Regardons comment accéder à la note d'économie de Marie avec cette syntaxe :

notes["Marie", "Economie"] #affiche 15

Cette syntaxe a l'avantage d'être bien plus lisible et facile à comprendre que la précédente. C'est pourquoi il est recommandé de nommer vos lignes et colonnes et de procéder ainsi pour selectionner des éléments. Cela rendra votre code plus facile à comprendre et donc à utiliser.

Remarque : Pour que cela fonctionne, vous devez faire attention à ce que chaque nom de ligne et de colonne soit unique. Si ce n'est pas le cas, R vous indiquera une erreur.

Selectionner plusieurs éléments

Il est également possible de selectionner plusieurs éléments dans une matrice. Pour cela, la syntaxe est identique à celle utilisée pour selectionner des éléments dans un vecteur. Elle s'applique juste pour les lignes ET les colonnes de la matrice. Il suffit d'indiquer un vecteur des lignes et colonnes à selectionner. Selectionnons les notes d'économie et de maths de Marie et de Pierre.

notes[c(1, 3), c(3, 4)]

Le résultat obtenu est la sous matrice suivante :

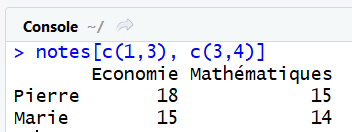
Selectionner plusieurs éléments nommés

Là encore, il est possible d'utiliser le nom des lignes et colonnes pour réaliser notre selection. Il nous suffit pour cela d'indiquer les noms de chaque ligne et colonne au lieu de leur numéro.

notes[c("Pierre", "Marie"), c("Economie", "Mathématiques")]

Le résultat est bien sur le même :

Cette seconde syntaxe est recommandée là aussi, car plus lisible. Le lecteur du code comprend imédiatement ce qui est selectionné ou pas.

Remarque : Les méthodes que nous avons vu pour les vecteur fonctionnent également. Par exemple vous pouvez utiliser des indices négatifs pour indiquer les colonnes à exclure (ma_matrice[(c(-1,-2), 2] ) et également utiliser la syntaxe avec le : pour parcourire un ensemble de lignes ou de colonnes (maMatrice[1:4,2] ).

Selection d'une ligne ou d'une colonne

Nous pouvons également selectionner entiérement une ligne ou une colonne. Pour cela, il suffit d'indiquer le numéro des lignes/colonnes qui nous intéressent, et de laisser la partie correspondants aux colonnes/lignes vide. Selectionnons les notes de Marie :

notes["Marie", ]

Voici le résultat obtenu :

Cela marche de même pour les colonnes, en laissant l'indice des lignes vides. Prennons les notes d'économie de tous les étudiants :

notes[, "Economie"]

Réaliser des opérations sur la ligne ou la colonne selectionnée

Il est souvent utile de réaliser des opérations sur des lignes ou des colonnes d'une matrice. Par exemple, on peut vouloir dans notre exemple de notes d'étudiants vouloir calculer la moyenne par étudiant ou par matiére. Pour cela, il nous suffit d'extraire la colonne ou ligne en question, et d'appliquer une fonction sur le vecteur obtenu.

Calculons la moyenne de notre Marie :

moyenne_marie = mean(notes["Marie",]) #affiche 14 de moyenne, plutôt pas mal !

De même, on peut calculer la moyenne des étudiants en philosophie :

moyenne_philo = mean(notes[, "Philosophie"]) #affiche 13

Ajouter des lignes et des colonnes

Il est parfois utile de pouvoir ajouter des lignes ou des colonnes à une matrice existante. Pour cela, il existe deux fonctions utiles : rbind() et cbind() . La premiére permet d'ajouter une ligne, et la seconde une colonne.

Regardons comment rbind() peut nous permettre d'ajouter une nouvelle élève à notre matrice.

notes = rbind(notes, c(12,15,14,15))

Remarquer que notre nouvelle matrice obtenu n'a pas de nom pour la nouvelle ligne. Ou plutôt, la nouvelle ligne à un nom vide.

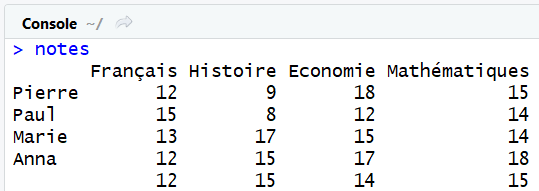
Nous pouvons alors utiliser la fonction rnames() pour ajouter un nouveau nom a notre 5éme ligne, comme ceci :

rownames(notes)[5] = "Julia"

Ajouter une colonne

Pour ajouter une colonne, nous procédons de la même façon, mais avec la fonction cbind() . Ajouter une note en philosophie à tous nos étudiants.

notes = cbind(notes, c(18,12,14,8,13))

Puis donner le nom de cette nouvelle matiére :

colnames(notes)[5] = "Philosophie"

Et voilà notre matrice de notes.

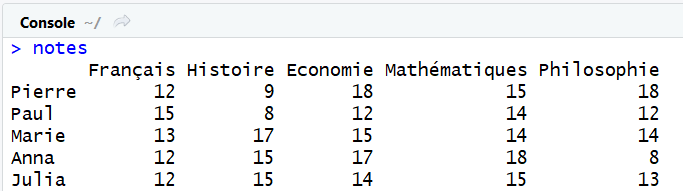
Fusionner des matrices par lignes

Les fonctions rbind() et cbind() peuvent aussi servir à fusionner des matrices, par le bas ou par la droite. Supposons que nous ayons une nouvelle matrice de notes à ajouter à notre matrice existante :

maxime = c(16,12,15,17,11)
lynda = c(14,14,12,13,15)
notes2 = matrix(data = c(maxime, lynda), nrow = 2)
#On nomme les lignes et les colonnes :
rownames(notes2) = c("Maxime", "Lynda")
colnames(notes2) = c("Français", "Histoire", "Economie", "Mathématiques", "Philosophie")

Nous aimerions bien ajouter ces deux étudiants à notre matrice existance notes pour regrouper l'ensemble des élèves dans une seule structure de données. Pour cela, on peut utiliser rbind() qui va fusionner les deux matrices par le bas, à condition qu'elles aient le même nombre de colonnes et que ces colonnes aient les mêmes noms (si elles en ont).

notes = rbind(notes, notes2)

Et voilà notre nouvelle matrice notes :

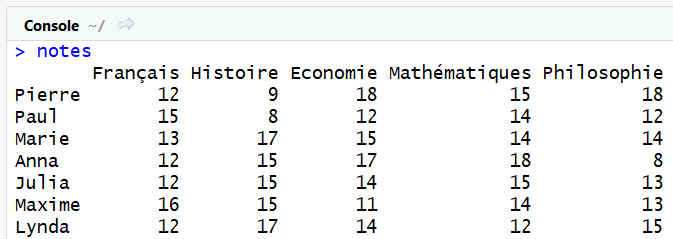
Fusionner les matrices par les colonnes

Il est possible de faire la même chose mais en fusionnant les matrices par les colonnes. Suposons pour cela que nous ayons une matrice comportant deux nouvelles matiéres et leurs notes pour l'ensemble des élèves :

sport = c(11, 12, 15, 14, 13, 15, 13)
art = c(13, 9, 10, 15, 12, 11, 8)
matieres = matrix(data = c(sport, art), nrow = 7)
rownames(matieres) = c("Pierre", "Paul", "Marie", "Anna", "Julia", "Maxime", "Lynda")
colnames(matieres) = c("Sport", "Art")

La nouvelle matrice de notes à ajouter ressemble à ceci :

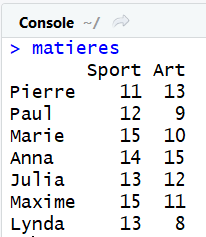
On peut maintenant fusionner la matrice notes avec cette nouvelle matrice matieres par la droite avec la fonction cbind() :

notes = cbind(notes, matieres)

Là encore, il faut faire attention à ce que le nombre de lignes entre les deux matrices corresponde et à ce que les noms des lignes soient aussi identiques. Sinon, la fusion ne fonctionnera pas. Voici la nouvelle matrice notes obtenue :

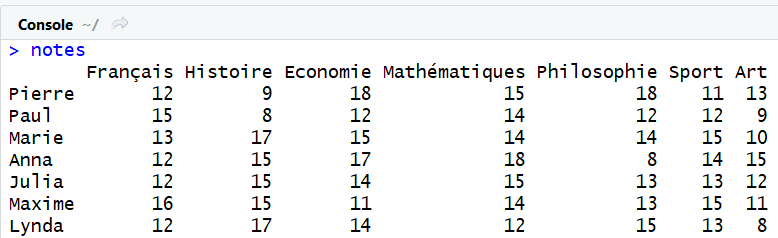
Opérations avec les matrices

Nous allons maintenant présenter comment réaliser les opérations de base de calcul matricielle en R. Bien entendu, cela demande de manipuler des matrices de nombre (integer , double ou complex ).

Transposer une matrice

R permet de facilement transposer une matrice, à l'aide de la fonction t() . Cette fonction fonctionne pour n'importe quelle matrice (composée de nombres ou non).

transposee = t(notes)

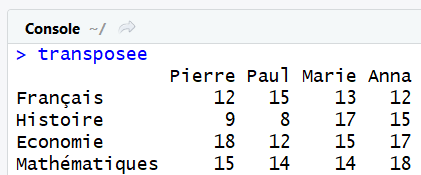
Opérations sur les matrices

Les opérations usuelles sur les matrices fonctionnent de la même façon qu'avec les vecteurs : elles se font membre à membre. Pour cela, il faut bien entendu que les deux matrices aient la même taille. Ainsi ajouter deux matrices de mêmes dimensions revient à ajouter chaque élément de la premiére matrice avec l'élément correspondant de la seconde matrice.

Voici un exemple avec l'addition :

a = matrix(data = 1:4, rnow = 2)
b = matrix(data = 1:4, nrow = 2)
print(a + b)

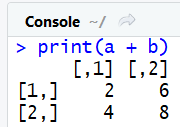
Cela fonctionne de même pour la soustraction, multiplication, modulo et toutes les autres opérations que nous avons vu au chapitre sur la manipulation des vecteurs.

Multiplication matricielle

Pour réaliser une multiplication matricielle au sens mathématique du terme, il faut utiliser l'opérateur %*% . Voici un exemple à partir des deux matrices précédentes.

print(a %*% b)

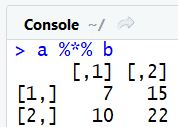
Inverser une matrice et résoudre un systéme

R posséde une fonction qui permet de trouver automatiquement et rapidement l'inverse d'une matrice carrée. Il s'agit de la fonction solve() .

solve(a)

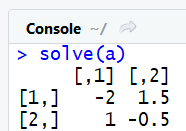
Si vous voulez résoudre un systéme d'équation du type Ax =b, vous pouvez utiliser le second paramétre de la fonction solve, comme ceci :

solve(A, b)

Cette fonction est très utile à connaitre si devez travailler avec des systémes de matrices et les résoudre.

Trouver les valeurs propres

R sait aussi trouver les valeurs et vecteurs propres associés à une matrice. Il utilise pour cela la fonction eigen() qui retourne une liste. Le premier élément de cette liste est les valeurs propres de la matrice et le second élément de la liste contient les vecteurs propres.

y = eigen(a)
y$values #affiche les valeurs propres
y$vectors #affiche les vecteurs propres

Autres opérations matricielles

Il existe un certain nombre d'autres opérations matricielles que R peut effectuer : triangulariser une matrice, faire une single value decomposition, calculer son inverse de Moore-Penrose, etc. Nous n'allons pas présenter toutes ces fonctions ici, mais vous pouvez les retrouver ici. Il existe également des packages qui permettent d'ajouter de nouvelles fonctions utiles au traitement matricielle.

A retenir :

Ce chapitre couvre les principes choses à savoir pour manipuler les matrices avec R :

Vous pouvez nommer les lignes et colonnes d'une matrice avec les fonctions rownames() et colnames().
Vous pouvez selectionner un élément par ses coordonnées dans la matrice ou par ses noms de ligne ou colonne si la matrice est nommées.
Vous pouvez selectionner une ligne ou colonne compléte avec matrice[i, ] ou matrice[, j] et appliquer des fonctions comme mean() au vecteur obtenu.
Il est possible de fusionner des matrices par les lignes ou les colonnes avec rbind() et cbind() . Ces fonctions permettent aussi d'ajouter un vecteur ligne ou colonne à une matrice. Dans le cas d'une matrice nommée, ce nouveau vecteur aura un nom vide associé à sa ligne ou colonne.
Les opérateurs mathématiques usuels appliqués aux matrices font les calculs membre à membre entre matrices de mêmes dimensions. L'opérateur %*% correspond a la multiplication matricielle mathématique.
R fournit un certain nombre de fonctions pour réaliser les opérations matricielles usuelles : inversion de matrice, transposée, résolution de systémes, extractions des vecteurs et valeurs propres, etc.

Manipuler les matrices